Содержание
Понятия перевода и перемещения
Как мы помним из предыдущей статьи в журнале «Я кадровик», перевод — это постоянное или временное изменение трудовых функций работника и/или его структурного подразделения, если оно указано в трудовом договоре, при продолжении работы у того же работодателя, а также перевод на работу в другую местность вместе с работодателем. В большинстве случаев перевод требует согласия работника.
При перемещении условия трудового договора не меняются, движение сотрудника внутри организации происходит без изменения трудовой функции. И, как видно из ч. 3 ст. 72.1 ТК РФ, перемещение не требует согласия работника и выполняется на усмотрение работодателя без заключения дополнительного соглашения с сотрудником.
Перемещение сотрудника в другое подразделение без изменения трудовой функции и условий работы также не требует оформления дополнительного соглашения, но только в том случае, если в трудовом договоре изначально не было указано структурное подразделение.
Важно! Работодатель не имеет права перемещать сотрудника на противопоказанную ему по состоянию здоровья работу.
Основные различия между переводом и перемещением
- Существенные условия договора: при переводе изменяются, при перемещении — нет. То есть перевод зачастую требует от сотрудника обладания специальными навыками, соответствующим образованием или квалификацией.
- Трудовая функция (профессия, специальность, квалификация, должность): при перемещении сотрудника она остается такой же, при переводе — меняется.
- Местность: если предполагается направить сотрудника работать в другое муниципальное образование или другой субъект Федерации, то это считается переводом. В рамках перемещения сотрудник остается работать в том же населенном пункте.
- Согласие работника: при переводе требуется, при перемещении — нет.
- Запись в трудовой книжке: обязательно оформляется при постоянном переводе. Перемещение этого не требует.
- Дополнительное соглашение: всегда заключается при переводе сотрудника. В документе оговариваются новые условия работы сотрудника.
 «Контур-Персонал» упрощает работу с приказами:
«Контур-Персонал» упрощает работу с приказами:
- содержит приказы о переводе (постоянном, временном);
- позволяет оформить приказ об изменении условий трудового договора (оплаты труда, графика работы, категории или разряда и т п.);
- помимо форм приказов содержит формы дополнительных соглашений.
Попробовать бесплатно программу «Контур-Персонал»
Если вы хотите перевести денежные средства другому физическому или юридическому лицу, то это можно сделать несколькими способами. Предлагаем разобраться, что такое денежные переводы и банковские платежи, в чем их преимущества и отличия.
Банковский перевод – это безналичная форма оплаты услуг, которая заключается в осуществлении платежа Плательщиком Получателю. Платеж можно производить несколькими способами, самым популярным из которых является электронный перевод, позволяющий быстро и эффективно перевести финансовые средства.
Давайте рассмотрим процесс отправки банковского перевода подробнее. Плательщик составляет особый платежный документ, предоставляющий право владельцу денежного счета давать указание банку по поводу безналичного перевода финансовых средств тому или иному клиенту другого банка (Получателю). Данный документ должен быть обязательно принят к исполнению. Банк не может отказать клиенту в операции, если на счету отправителя имеются денежные активы, позволяющие осуществить транзакцию. При составлении исполняемого документа необходимо обязательно указывать реквизиты физических и юридических лиц, участвующих в процессе банковского перевода.
При оформлении банковского перевода следует внимательно проверять все свои идентификационные данные и стараться не терять выданные банком реквизиты, т.к. в случае неверного или неполного указания даже одного реквизита финансовое учреждение может отказать в операции и потребовать от Плательщика предоставления правильных сведений.
В процессе осуществления банковского перевода количество денежных средств на счету Плательщика уменьшается ровно настолько, насколько оно увеличивается на счету Получателя. Кроме того, банк может потребовать от клиента оплатить комиссионный сбор, определяемый видом предоставляемой услуги и размером денежных активов, которые переводятся из одного места в другое.
Срок успешного выполнения операции составляет от 1 до 3 дней и зависит от времени принятия оператором распоряжения клиента. После того, как денежные средства будут сняты со счета Плательщика, оператор обязан незамедлительно сообщить ему об этом. В случае, же если оператор не направил клиенту такое подтверждение, финансовая операция считается не завершенной и может быть аннулирована. Что же касается денежных обязательств Плательщика, то они полностью прекращаются после того, как средства поступили на счет Получателя.
В настоящее время, в банковской системе можно выделить несколько видов переводов, каждый из которых имеет свою специфику и правила осуществления. Рассмотрим подробнее межбанковские и межфилиальные переводы.
1. Межбанковский перевод – это процесс безналичного перевода финансовых активов из одного банка в другой. Для осуществления такого рода операции каждому банковскому учреждения необходимо открыть личные корреспондентские счета в Центральном Банке РФ. Счета данного типа представляют собой открытые счета, содержание которых отображает все денежные расчеты между банками.
При межбанковском переводе затрачивается довольно длительное время.
Обращаем внимание на то, что банковское учреждение не несет никакой ответственности за те сведения, которые указаны в платежном поручении. Банк лишь принимает документ к исполнению, а инициирующим лицом является сам владелец финансовых активов.
2. Межфилиальный перевод — это денежная операция, которая осуществляется между двумя филиалами одного банка при помощи метода безналичного расчета.
Несмотря на то, что межфилиальный перевод также проводится через корреспондентский счет, скорость его осуществления намного выше, нежели у перевода межбанковского, так как для проведения транзакций используются внутренние счета.
Суть межфилиального перевода заключается в следующем. В рамках действующего платежного поручения, составленного отправителем, банковское учреждение списывает указанную в документе денежную сумму со счета отправителя и отправляет ее на свой внутренний счет. Далее, деньги переводятся в другой филиал, который, в свою очередь, гарантирует зачисление перевода на счет получателя.
Межфилиальный перевод может использоваться и самим банком том случае, когда одному из отделений срочно требуются финансовые средства на выплату денежного вклада большого размера. Таким образом, банки всегда застрахованы от возникновения недостатка капитала и могут выполнять свои обязательства перед клиентами в полном объеме.
Главным и неоспоримым преимуществом банковских переводов является их быстрота и безопасность. Благодаря электронным транзакциям любой клиент банка может перечислять денежные средства в любую нужную ему точку мира в самые кратчайшие сроки. Для этого достаточно прийти в ближайшее отделение банка и обратиться к тому сотруднику финансового учреждения, который занимается переводами. Процесс осуществления транзакции, как правило, осуществляется мгновенно и лишь в отдельных случаях занимает от 1 до 3 рабочих дней.
Заказать банковский перевод можно в любом банке. Процедура оформления электронного платежа довольно проста и не требует каких-либо знаний. Опытные сотрудники финансового учреждения внимательно выслушают ваши запросы и оформят всю необходимую для перевода документацию.
Теперь рассмотрим подробнее денежные переводы.
Денежный перевод — это перечисление одним лицом денежных средств другому частному лицу, обычно через какую-либо специальную систему денежных переводов и без открытия счета в банке.
Системы денежных переводов представляют собой определенную альтернативу традиционному платежу через банки.
На практике системы денежных переводов работают по следующей схеме. Клиент приходит в компанию или банк — участник системы денежных переводов, заполняет заявку, вносит через кассу деньги и получает оригинальный код. Его необходимо сообщить Получателю. Владея кодом, человек может получить отправленную сумму в любой точке планеты, где существует филиал компании.
Как правило, системы денежных переводов имеют широкую сеть представительств, отличающие их от традиционных кредитных учреждений.
Наиболее известные участники рынка — такие системы, как UNIStream, «Анелик», «Золотая Корона — Денежные переводы», MoneyGram, «Аллюр», «Блиц», InterExpress, Contact, «Лидер», Blizko, «Быстрая Почта», Western Union, Coinstar (Travelex) Money Transfer, «КиберДеньги», PrivatMoney.
Помимо этих компаний традиционным участником сегмента является Почта России, имеющая свои представительства во всех даже самых отдаленных регионах.
Для того чтобы воспользоваться системой денежных переводов, необходимо, во-первых, выбрать те из них, которые имеют подразделения в городе, где предполагается получение денег. А во-вторых, сравнить комиссии за операции, т. к. они могут существенно различаться.
Платой за простоту и доступность системы денежных переводов служит их более высокая по сравнению с традиционными платежами между банками стоимость, которая в среднем составляет от 2% до 6% от суммы.
В отличие от традиционных кредитных учреждений системы денежных переводов, как правило, имеют широкую сеть представительств.
Второе существенное отличие — системы денежных переводов чаще всего ориентированы на совершение транзакций без открытия расчетных счетов, что упрощает процедуру для клиентов и сокращает документооборот.
☰
На первый взгляд перемещение и путь — близкие по смыслу понятия. Однако в физике между перемещением и путем есть ключевые отличия, хотя оба понятия связаны с изменением положения тела в пространстве и нередко (обычно при прямолинейном движении) численно равны друг другу.
Чтобы понять отличия перемещения и пути, дадим сначала им определения, которыми их наделяет физика.
Перемещение тела — это направленный отрезок прямой (вектор), начало которого совпадает с начальным положением тела, а конец совпадает с конечным положением тела.
Путь тела — это расстояние, которое прошло тело за определенный промежуток времени.
Представим себе, что вы стали у своего подъезда в определенную точку. Обошли дом и вернулись в исходную точку. Так вот: ваше перемещение будет равно нулю, а путь — не будет. Путь будет равен длине кривой (например, 150 м), по которой вы шли вокруг дома.
Однако вернемся к системе координат. Пусть точечное тело двигается прямолинейно из точки A с координатой x0 = 0 м в точку B с координатой x1 = 10 м. Перемещение тела в данном случае составит 10 м. Так как движение было прямолинейным, то 10-ти метрам будет равен и проделанный телом путь.
Если же тело прямолинейно двигалось из начальной (A) точки с координатой x0 = 5 м, в конечную (B) точку с координатой x1 = 0, то его перемещение составит -5 м, а путь 5 м.
Перемещение находится как разность, где из конечной координаты вычитают начальную. Если конечная координата меньше начальной, т. е. тело двигалось в обратном направлении по отношению к положительному направлению оси X, то перемещение будет отрицательной величиной.
Так как перемещение может иметь как положительное, так и отрицательное значение, то перемещение является векторной величиной. В отличие от него, путь — всегда положительная или равная нулю величина (путь — скалярная величина), так как расстояние не может быть отрицательным в принципе.
Рассмотрим еще один пример. Тело прямолинейно двигалось из точки A (x0 = 2 м) в точку B (x1 = 8 м), далее также прямолинейно из B переместилось в точку C с координатой x2 = 5 м. Чему равны и отличаются ли общий путь (A→B→C) проделанный данным телом и его суммарное перемещение?
Общий путь вычисляется путем сложения двух расстояний, прошедших телом. Расстояние от точки A до B составляет 6 м, а от B до C тело проделало путь в 3 м. Итого получаем 9 м.
Таким образом, в данной задаче путь и перемещение тела отличаются между собой.
Рассмотренная задача не совсем корректна, так как необходимо указывать моменты времени, в которые тело находится в определенных точках. Если x0 соответствует момент времени t0 = 0 (момент начала наблюдений), то пусть например x1 соответствует t1 = 3 c, а x2 соответствует t2 = 5 c. То есть промежуток времени между t0 и t1 составляет 3 с, а между t0 и t2 составляет 5 с. В этом случае получается, что путь тела за промежуток времени в 3 секунды составил 6 метров, а за промежуток в 5 секунд — 9 метров.
В определении пути фигурирует время. В отличие от него для перемещения время не имеет особого значения.
При своем движении материальная точка описывает некоторую линию, которую называют ее траекторией движения. Траектория может быть прямой линией, а может представлять собой кривую.
Путь
Определение
Путь — длина участка траектории, который прошла материальная точка за рассматриваемый отрезок времени. Путь — это скалярная величина.
При прямолинейном движении в одном направлении пройденный путь ($\Delta s$) равен модулю изменения координаты тела. Так, если тело двигалось по оси X, то путь можно найти как:
\
где $x_1$ — координата начального положения тела; $x_2$ — конечная координата тела.
Его можно вычислить, если известен модуль скорости ($v=v_x$):
\
где $t$ — время движения тела.
Графиком, который отображает зависимость пути от времени при равномерном прямолинейном движении, является прямая (рис.1). С увеличением величины скорости увеличивается угол наклона прямой относительно оси времени.
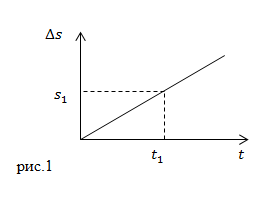
Путь не бывает меньше нуля и не может уменьшаться при движении тела.
Перемещение
Определение
Перемещением называют вектор, который проводят из начального положения движущейся материальной точки в ее конечное положение:
\
Вектор перемещения численно равен расстоянию между конечной и начальной точками и направлен от начальной точки к конечной.
Приращение радиус-вектора материальной точки — это перемещение ($\Delta \overline{r}$).
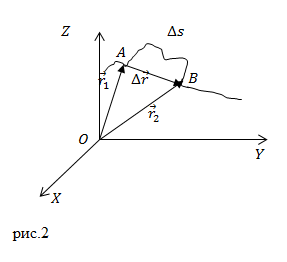
В декартовой системе координат радиус-вектор точки представляют в виде:
\
где $\overline{i}$, $\overline{j}$,$\ \overline{k}$ — единичные орты осей X,Y,Z. Тогда $\Delta \overline{r}$ равен:
\\overline{i}+\left\overline{j}+\left\overline{k}\left(5\right).\]
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина вектора перемещения равна пройденному точкой пути:
\
Если тело совершает несколько перемещений, то их можно складывать по правилам сложения векторов:
\
Если направление движения тела изменяется, то модуль вектора перемещения не равен пройденному телом пути.
Примеры задач на путь и перемещение
Пример 1
Задание: Мяч бросили вертикально вверх от поверхности Земли. Он долетел до высоты 20 м. и упал на Землю. Чему равен путь, который прошел мяч, каков модуль перемещения?
Решение: Сделаем рисунок.
В нашей задаче мяч движется прямолинейно сначала вверх, затем вниз. Так как путь — длина траектории, то получается, что мяч дважды прошел расстояние h, следовательно:
\
Перемещение — направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю:
\
Ответ: $\ Путь\ \Delta s=2h$. Перемещение $\Delta r=0$
Пример 2
Решение: Сделаем рисунок.
Радиус — вектор начальной точки запишем как:
\
Радиус — вектор конечной точки имеет вид:
\
Вектор перемещения представим как:
- Основные теоретические сведения
- Система СИ
- Путь и перемещение
- Средняя скорость
- Равноускоренное прямолинейное движение
- Свободное падение по вертикали
- Горизонтальный бросок
- Бросок под углом к горизонту (с земли на землю)
- Сложение скоростей
- Равномерное движение по окружности
Основные теоретические сведения
Система СИ
К оглавлению…
Основные единицы измерения величин в системе СИ таковы:
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Таблица дольных и кратных приставок в физике:
Путь и перемещение
К оглавлению…
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
К оглавлению…
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: Lполн – весь путь, который прошло тело, tполн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
К оглавлению…
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:
Свободное падение по вертикали
К оглавлению…
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
К оглавлению…
При горизонтальном броске с начальной скоростью v0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:
При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали. Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
К оглавлению…
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):
Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
К оглавлению…
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
К оглавлению…
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:
При равномерном вращении скорость тела будет определяется следующим образом:
где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt. Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Связь между модулем линейной скорости v и угловой скоростью ω:
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:
Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.




